An easier way to screenshot UAC prompt on windows
Usually, print screen key or short cut of taking screenshot like Win+Shift+S don't work while UAC prompt appears. So, I googled it and hit some blog articles that describe the ways to take screenshot as follows
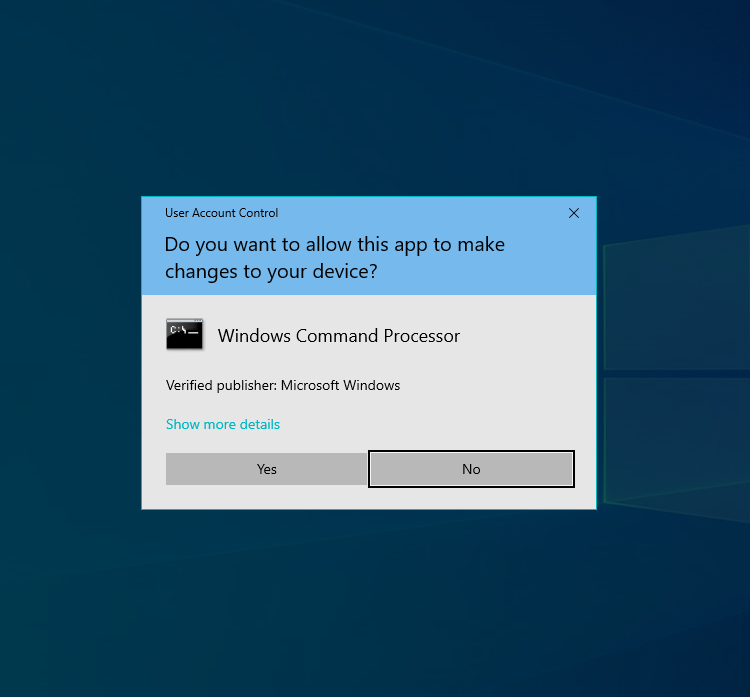
But I found another way that doesn't need changing security level temporary and it's really easy. And it can snip screenshot range includes gray out background like below. Please notice that I verified this way in my environment only. This may not work in other environments.
Steps
- Open "snip & sketch" tool
- Select "Snip in 10 seconds" from pulldown menu under the "New"
- Do something it displays UAC prompt (let's say opening command prompt as administrator) within 10 seconds
- Wait few seconds until "Snip & sketch" takes delayed screenshot
- You will see something action like a yellow frame is shown at the edge of screen that means the tool took a screenshot.
- Now, you can close UAC prompt. Choose Yes or No as you like.
- Then, you will see "Snip & sketch" tool is waiting your operation to snip from screenshot.
- After select it, you can save it as a file.
That's it! A screencast is here (Although, actual UAC prompt wasn't recorded in screencast...)
より簡単なユーザーアカウント制御画面のスクリーンショット撮影法
通常のプリントスクリーンキーやショートカットによるスクリーンショットではユーザーアカウント制御画面(UAC画面)のキャプチャは出来ないわけでして、なにか良い方法は無いかと検索してみたところ、幾つかの記事が見つかりました。例えば
といったところでしょうか。いずれもセキュリティレベルを下げたり、リモートデスクトップを利用したりと、少々大掛かりな方法なので一歩引いていたんですが、他に簡単な方法がありましたのでそれについての手順の説明です。
但し、様々な環境下で検証した訳ではないので、この通りでうまく行かない環境もあるかもしれません。実際に撮ってみたスクリーンショットは以下のような感じになります。

手順
- "切り取り&スケッチ" ツールを開く
- "新規"のプルダウンから、"10秒後に切り取り"を選択
- UAC画面が出てくるような操作(コマンドプロンプトを管理者権限で開くなど)を10秒以内に行う
- UAC画面が出たら、"切り取り&スケッチ"ツールがスクリーンショットを取るまで数秒待つ(画面端に黄色いフレームが現れるなど、なんらかのアクションがあると思います)
- UAC画面を閉じます。"はい"か"いいえ"、お好きな様に選んでUAC画面を閉じてください。
- "切り取り&スケッチ"ツールが、切り取り範囲を選択されるのを待ってる画面が現れます
- 必要な範囲を切り取って、ファイルに保存します
以上です。動画は以下の通りです。(実際のUAC画面はスクリーンキャストには映らなかったようですが…)

raspberry pi3への64bit版opensuseインストールとwifiの有効化
この記事は以前に書いた
Installing 64bit openSUSE to raspberry pi 3 - わらばんし仄聞記
After installing 64bit openSUSE to raspberry pi 3 - わらばんし仄聞記
を日本語化して整理したものです。
追記 2017/02/03
元々英語版の記事を書いていた時に使用したOSイメージである openSUSE-Tumbleweed-ARM-JeOS-raspberrypi3_aarch64.aarch64-2016.10.15-Build6.1.raw.xz での手順となります。その後この日本語版を書く際に使用してみたこの時点の最新版である openSUSE-Tumbleweed-ARM-JeOS-raspberrypi3.aarch64-2017.01.31-Build1.1.raw.xz でも試してみた所、この手順ではwlan0を認識してくれませでした。原因は調査中です。
追記 2017/02/05
Tumbleweed版ではなくLeap42.2版のJeOSイメージでは現時点での最新版で動作したとのことです。b4_dooms_dayさん、検証ありがとうございました!
その情報を元に自分の手元でも試してみた所、本記事本文のやり方でSDカードへの書き込み後、raspi3へセットしての最初の起動時はwlan0を何も設定していなくても認識していました。ですが、再起動したらwlan0が現れなくなり、その後は下で記した手順を経たら認識するようになりました。
はじめに
raspberry pi3を買ってみたものの、下調べが足りずにその時点でraspbianが64bit対応してなかったことを把握してませんでした。とはいえ、折角の64bitマシンなのにOSは32bitで動かすなんて悔しすぎる!
というわけで、raspberry pi3向けのイメージを探し求めた結果、openSUSEならば対応しているのを見つけ、これで動かしてやろうと思った次第です。
但し、自分が試した段階ではopenSUSEがinstallした直後の状態ではwifi用のNICを認識してくれず、これまたraspberry pi3なのにwifi使えないなんて悔しすぎる!ということでそこら辺まで動作するようにした際のメモです。
尚、SDカードに書き込みをしたりするのに使ってるのもopenSUSEを入れてあるラップトップだったりします。
After installing 64bit openSUSE to raspberry pi 3
Below are what I did after installing this OS to raspberry pi 3.
update 2017/02/03
About wifi device recognition, this was work on old OS image (openSUSE-Tumbleweed-ARM-JeOS-raspberrypi3_aarch64.aarch64-2016.10.15-Build6.1.raw.xz) as of wrote this article.
Latest OS image doesn’t recognize it by following steps.
update 2017/02/05
Latest version of Leap42.2 (as of 2017/02/05. file name is openSUSE-Leap42.2-ARM-JeOS-raspberrypi3.aarch64-2017.02.02-Build1.2.raw.xz) recognize wlan0 device by following article. Thank you b4_dooms_day san for validation!
extend main system partition
main partition of /dev/mmcblk0p2 had only 1.3GB of partition
nohostname:~ # df -hT Filesystem Type Size Used Avail Use% Mounted on devtmpfs devtmpfs 389M 0 389M 0% /dev tmpfs tmpfs 393M 0 393M 0% /dev/shm tmpfs tmpfs 393M 352K 393M 1% /run tmpfs tmpfs 393M 0 393M 0% /sys/fs/cgroup /dev/mmcblk0p2 ext4 1.3G 1.2G 0 100% / /dev/mmcblk0p1 vfat 200M 3.2M 197M 2% /boot/efi tmpfs tmpfs 79M 0 79M 0% /run/user/0
This isn’t enough so extend this partition.
nohostname:~ # fdisk /dev/mmcblk0 Welcome to fdisk (util-linux 2.28.2). Changes will remain in memory only, until you decide to write them. Be careful before using the write command. Command (m for help): p Disk /dev/mmcblk0: 29.7 GiB, 31914983424 bytes, 62333952 sectors Units: sectors of 1 * 512 = 512 bytes Sector size (logical/physical): 512 bytes / 512 bytes I/O size (minimum/optimal): 512 bytes / 512 bytes Disklabel type: dos Disk identifier: 0x495bfe7e Device Boot Start End Sectors Size Id Type /dev/mmcblk0p1 2048 411651 409604 200M c W95 FAT32 (LBA) /dev/mmcblk0p2 413696 61304040 60890345 29G 83 Linux /dev/mmcblk0p3 61304832 62332199 1027368 501.7M 82 Linux swap / Solari
This partition seems have 29GB of space. so I executed command such as below
# resize2fs /dev/mmcblk0p2 29G
wifi device recognition
I referred to following links
TUMBLEWEED Wifi (Broadcom 43438) not work on Raspberry Pi 3
Re: [opensuse-arm] Still no wlan on Raspberry 3
As of now, the distributed opensuse image for raspberry pi3 doesn’t recognize wifi device by default. I could recognize wifi device by process that was written in the bottom one of above two links. And I setup wlan0 by yast after that.
Running /usr/sbin/install-brcmfmac command may output warning message /usr/sbin/install-brcmfmac: line 4: warning: command substitution: ignored null byte in input because /sys/firmware/devicetree/base/compatible include null byte character.
Installing 64bit openSUSE to raspberry pi 3
I got raspberry pi 3 but I found out after got it that raspbian doesn't support aarch64. So I looked for distribution that works with 64bit linux on this raspberry pi and I have found opensuse fullfill my demand for now.
Official page is HCL:Raspberry Pi3 - openSUSE.
This official page uses serial port and HDMI display in step 3 and 4 but I didn't use these.
First, copy the OS image to SD card according to step 1 and 2. After this, you get a SD card that opensuse was installed.
Next, mount this SD card on another linux OS. In this case, I used my laptop which was installed opensuse. In my case, SD card is mounted to /dev/mmcblk0 so I executed command like below.
# mount /dev/mmcblk0p2 /mnt
second partition was system partition so I mount it to /mnt and edit some files.
As of now, I aim to just work and accessible through ssh so I don't care security. Because of this, I stopped firewall and start sshd like below.
# echo "service sshd start" >> /mnt/etc/init.d/after.local # echo "systemctl stop SuSEfirewall2" >> /mnt/etc/init.d/after.local
And edit /etc/ssh/sshd_config for permit login with root user and password authentication.
--- /etc/ssh/sshd_config.org 2016-10-17 18:47:58.143853990 +0200 +++ /etc/ssh/sshd_config 2016-10-16 11:25:12.849113103 +0200 @@ -46,7 +46,7 @@ # Authentication: #LoginGraceTime 2m -#PermitRootLogin yes +PermitRootLogin yes #StrictModes yes #MaxAuthTries 6 #MaxSessions 10 @@ -74,7 +74,7 @@ #IgnoreRhosts yes # To disable tunneled clear text passwords, change to no here! -#PasswordAuthentication no +PasswordAuthentication yes #PermitEmptyPasswords no # Change to no to disable s/key passwords
After boot raspberry pi 3, it will make connection with DHCP so we need to find IP of the raspberry pi. You can find it by nmap command such as
$ nmap -p22 192.168.1.0/24
Please replace local IP for your environment. After this, you need to boot raspberry pi 3 and access with root user. If you can find the row that is "22/tcp open ssh" you can access by ssh to it raspberry pi.
Nmap scan report for 192.168.1.6 Host is up (0.0068s latency). PORT STATE SERVICE 22/tcp open ssh MAC Address: B8:27:EB:FD:AB:BE (Raspberry Pi Foundation)
KDEにて指定したvirtual desktop上にアプリケーションを自動起動
最近、メインマシンのOSをopenSUSEのTumbleweedに変えました。 デスクトップ環境はKDEを使用してます。バージョンは以下の通り。
$ kstart --version
Qt: 4.8.7
KDE Development Platform: 4.14.14
KStart: 4.14.12
以前使ってたバージョンでは、前回終了時に起動してたアプリケーションが次回起動時に元のvirtual desktop上で起動されてるのが良かったんだけど、なんか今回からそうなってはくれない。コンソールなんかはどうせ毎回確実に開くのに、逐一起動するのはめんどい。あとフルスクリーンにしたりと。
単純に、起動時に自動的にコマンドを実行させるには [System Settings] -> [Workspace] -> [Startup and Shutdown] から、Autostartに設定を追加してやればいい。
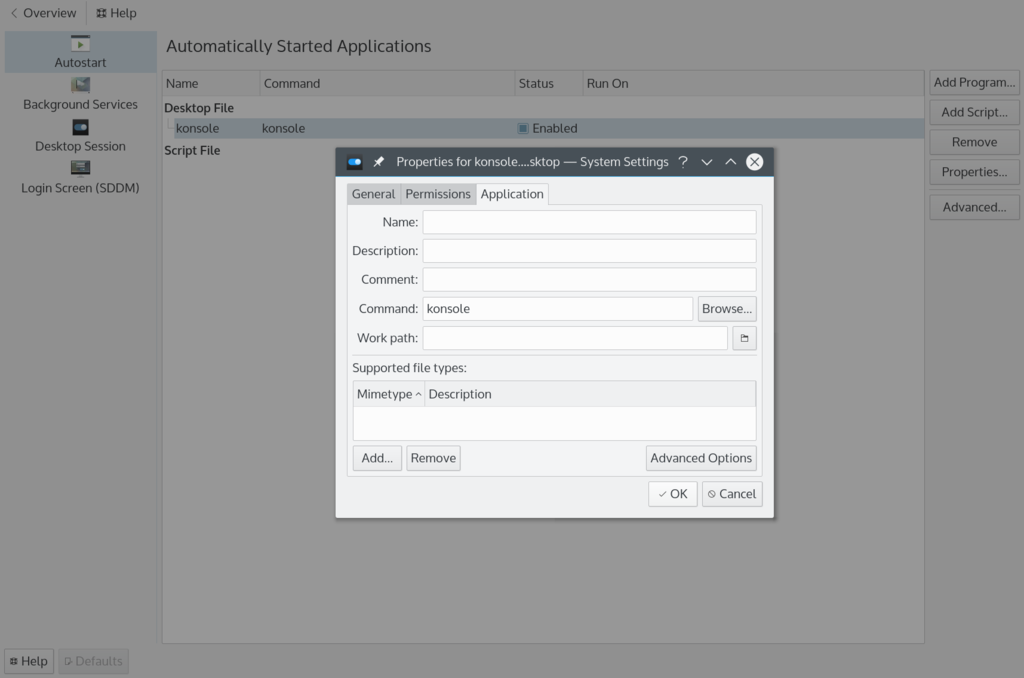
ただし、これだと何処のvirtual desktopに起動するかは指定出来てないので、適当な所に起動されてしまう。それに、通常のwindowで開かれるので、full screenにしたりするのまだめんどい。
この問題を解消するにはコマンド部分を修正して、kstart経由で実行すると良い。
$ kstart --desktop 1 --fullscreen konsole --hide-menubar
こんな感じ。これを先ほどのcommandフォームに指定してやればOK。
参考:autostart application on specific virtual desktop • KDE Community Forums
初心者の為の線形代数勉強会(2)
前回に続き、初心者のための線形代数勉強会(3) - connpass に参加してきました。今回は第二章の以下の節をやりました
- 2.4 行列の転置と共役
- 2.5 行列の分割
- 2.6 行列の線形写像
前回のエントリは下記の通りです
2.4 行列の転置と共役
基本的には教科書参照。転置行列、対称行列、交代行列についての説明。任意の正方行列が1つの対称行列と1つ交代行列の和として一意に表せることなどについてが前半部分。この辺りは教科書に書かれてる事そのままなので、特筆する事は無し。
命題2.4.2で転置についての性質が示されていたが、\({}^t\!(AB)={}^t\!B{}^t\!A\)ってなんか群の性質でも見かけたような気が・・・。
後半は実行列、複素行列、実ベクトル、複素ベクトル、複素共役行列、随伴行列(エルミート共役)などについて。
この節については教科書を参照すれば事足りるかと思うので、ここでは触れません。
2.5 行列の分割
例 2.5.1
\((m,n)\)型行列\(A\)の各列および各行をベクトルと見なして
\begin{align*} A = \begin{pmatrix}\boldsymbol{a_1} & \boldsymbol{a_2} & \cdots & \boldsymbol{a_n} \end{pmatrix} = \begin{pmatrix}\boldsymbol{a'_1} \\ \boldsymbol{a'_2} \\ \vdots \\ \boldsymbol{a'_n} \end{pmatrix} \end{align*}
で表す事がある。とのことですが、確かに文と式をちゃんと読めばその通りなんですが、初見殺しな感じがしますね。要は

こんな\((m,n)\)型行列について、例えば各列、つまり青枠の要素をそれぞれ1つの列ベクトルとして考えると、列ベクトルが並んだ\((1, n)\)型の行列と見なせますね。それが
\begin{align*} A = \begin{pmatrix}\boldsymbol{a_1} & \boldsymbol{a_2} & \cdots & \boldsymbol{a_n} \end{pmatrix} \end{align*}
なわけですね。同様のことが行についても考えられます。
例 2.5.2
\((m,n)\)型行列\(A\)、\((n,r)\)型行列\(B\)をそれぞれ行ベクトルと列ベクトルで表して
\begin{align*} A = \begin{pmatrix}\boldsymbol{a'_1} \\ \boldsymbol{a'_2} \\ \vdots \\ \boldsymbol{a'_n} \end{pmatrix},~~ B = \begin{pmatrix}\boldsymbol{b_1} & \boldsymbol{b_2} & \cdots & \boldsymbol{b_r} \end{pmatrix} \end{align*}
とすれば
\begin{align*} AB = \begin{pmatrix} \boldsymbol{a'_1}\boldsymbol{b_1} & \boldsymbol{a'_1}\boldsymbol{b_2} & \dots & \boldsymbol{a'_1}\boldsymbol{b_r} \\ \boldsymbol{a'_2}\boldsymbol{b_1} & \boldsymbol{a'_2}\boldsymbol{b_2} & \dots & \boldsymbol{a'_2}\boldsymbol{b_r} \\ \vdots & \vdots & \ddots& \vdots \\ \boldsymbol{a'_m}\boldsymbol{b_1} & \boldsymbol{a'_m}\boldsymbol{b_2} & \dots & \boldsymbol{a'_m}\boldsymbol{b_r} \end{pmatrix} \end{align*}
で表せ、これは各項がスカラーとなっている。
一方、\(A, B\)をそれぞれ列ベクトルと行ベクトルで
\begin{align*} A = \begin{pmatrix}\boldsymbol{a_1} & \boldsymbol{a_2} & \cdots & \boldsymbol{a_n} \end{pmatrix},~~ B = \begin{pmatrix}\boldsymbol{b'_1} \\ \boldsymbol{b'_2} \\ \vdots \\ \boldsymbol{b'_n} \end{pmatrix} \end{align*}
とすれば
\begin{align*} AB = \boldsymbol{a}_1\boldsymbol{b}'_1 + \boldsymbol{a}_2 \boldsymbol{b}'_2 + \dots + \boldsymbol{a}_n\boldsymbol{b}'_n \end{align*}
で表せ、この場合は各項が\((m, r)\)型の行列となっている。つまり、結果の見た目がかなり異なっているが、実質はどちらも\((m, r)\)型の行列となっている。
例 2.5.8
\(A\)、\(B\)ともに、行、列どちらも\(r\)個と\(s\)個の要素に分割されたブロックを持つ(\(A_{11}\)が\((r, r)\)型、\(A_{12}\)が\((r, s)\)型という具合。\(B\)についても同様)、例2.5.7の行列
\begin{align*} A = \begin{pmatrix} A_{11} & A_{12} \\ O & A_{22}\end{pmatrix}, ~~~ B = \begin{pmatrix} B_{11} & B_{12} \\ B_{21} & B_{22}\end{pmatrix} \end{align*}
について、\(A_{12} = O\)とするということで、つまり\(A\)の非対角成分は0となる。このとき、\(AB = BA = I_n~~~(n=r+s)\)であるとするということなので、要は\(B = A^{-1}\)である場合の\(B\)の各成分がどうなるかということですね。ということで、\(B\)の各成分を求めていきます。
\(I_n\)はまた、\(A, B\)を分割したように\(r\)個の要素と\(s\)個の要素でブロックに分けると
\begin{align*} I_n = \begin{pmatrix} I_r & O \\ O & I_s\end{pmatrix} \end{align*}
と表せる。一方、\(A\)と\(B\)について、この積\(AB\)は
\begin{align*} AB = \begin{pmatrix} A_{11}B_{11}+A_{12}B_{21} & A_{11}B_{12}+A_{12}B_{22} \\ A_{22}B_{21} & A_{22}B_{22}\end{pmatrix} \end{align*}
となり、題意の条件\(A_{12}=O\)より
\begin{align*} AB = \begin{pmatrix} A_{11}B_{11} & A_{11}B_{12} \\ A_{22}B_{21} & A_{22}B_{22}\end{pmatrix} \end{align*}
である。\(AB\)と\(I_n\)をそれぞれ比較して
\begin{align*} A_{11}B_{11} = B_{11}A_{11} = I_r,\,\,A_{22}B_{22} = B_{22}A_{22} = I_s,\,\,A_{11}B_{12} = O,\,\,A_{22}B_{21} = O \end{align*}
なので、\(B_{11} = A_{11}^{-1}\)、\(B_{22} = A_{22}^{-1}\)である。
また、\(A\)が正則行列の場合、\(AX = O\)ならば\(X = O\)であるから、\(A_{11}B_{12} = O\)より\(B_{12} = O\)。同様にして、\(B_{21} = O\)である。よって
\begin{align*} B = \begin{pmatrix} B_{11} & B_{12} \\ B_{21} & B_{22}\end{pmatrix} = \begin{pmatrix} A_{11}^{-1} & O \\ O & A_{22}^{-1}\end{pmatrix} = A^{-1} \end{align*}
以降、一般の場合についての記述は教科書参照。
2.6 行列と線形写像
例 2.6.1
\(\boldsymbol{x} \in \boldsymbol{R}^n\)の\(\boldsymbol{x}\)とは、要は\((n, 1)\)型の列ベクトルであるから、\(A\)が\((m, n)\)型行列の場合
\begin{align*} f(\boldsymbol{x}) = A\boldsymbol{x} \end{align*}
とすると、\(A\boldsymbol{x}\)は\((m, 1)\)型の列ベクトルとなり、\(\boldsymbol{R}^n\)から\(\boldsymbol{R}^m\)への線形写像となっている。この\((m, 1)\)型の列ベクトルを記述してみると
\begin{align*} A\boldsymbol{x} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{1n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} = \begin{pmatrix} \sum_{k=1}^{n} a_{1k}x_k \\ \sum_{k=1}^{n} a_{2k}x_k \\ \vdots \\ \sum_{k=1}^{n} a_{mk}x_k \end{pmatrix} \end{align*}
となる。
基本ベクトル
\(\boldsymbol{R}^{n}\)のベクトル(=\((n, 1)\)型の列ベクトル)について、各\(j\,(1 \leq j \leq n)\)に対して\(j\)番目の成分が1で、他の成分が全て0であるベクトルを\(\boldsymbol{e}_j\)とする。
\begin{align*} \boldsymbol{e_1} = \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix},~~~ \boldsymbol{e_2} = \begin{pmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{pmatrix},~~~ \ldots \boldsymbol{e_n} = \begin{pmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{pmatrix} \end{align*}
各成分の単位元みたいな感じですね。
写像\(f: \boldsymbol{R}^n \to \boldsymbol{R}^m\)が線形写像である場合
\begin{eqnarray} f(x) & = & f(x_1\boldsymbol{e}_1 + x_2\boldsymbol{e}_2 + \ldots + x_n\boldsymbol{e}_n) \\ & = & f(x_1\boldsymbol{e}_1) + f(x_2\boldsymbol{e}_2) + \ldots + f(x_n\boldsymbol{e}_n) \\ & = & x_1f(\boldsymbol{e}_1) + x_2f(\boldsymbol{e}_2) + \ldots + x_nf(\boldsymbol{e}_n) \\ & = & \begin{pmatrix} f(\boldsymbol{e}_1) & f(\boldsymbol{e}_2) & \ldots & f(\boldsymbol{e}_n) \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} \end{eqnarray}
なので、\(f(\boldsymbol{x}) = A\boldsymbol{x}\)であるとき、\(A = \begin{pmatrix} f(\boldsymbol{e}_1) & f(\boldsymbol{e}_2) & \ldots & f(\boldsymbol{e}_n) \end{pmatrix}\)と表せる。
これをふまえて問 2.11の(1)を考えると
\begin{align*} f\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 2x_1+3x_2 \\ x_1-5x_2 \\ 7x_1+6x_2 \end{pmatrix} \ldots (*) \end{align*}
について、線形写像\(f\)に対応する行列を求めろということなので、求める行列を\(A\)とすると、左辺は
\begin{eqnarray} f\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} & = & \begin{pmatrix} f(\boldsymbol{e}_1) & f(\boldsymbol{e}_2) \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \\ & = & \begin{pmatrix} f\begin{pmatrix} 1 \\ 0 \end{pmatrix} & f\begin{pmatrix} 0 \\ 1 \end{pmatrix} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \end{eqnarray}
となるので
\begin{align*} A = \begin{pmatrix} f\begin{pmatrix} 1 \\ 0 \end{pmatrix} & f\begin{pmatrix} 0 \\ 1 \end{pmatrix} \end{pmatrix} \end{align*}
である。なので、\(A\)の各成分を式\((*)\)に当てはめてみると
\begin{align*} f\begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \\ 7 \end{pmatrix}, \,\,\, f\begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 3 \\ -5 \\ 6 \end{pmatrix} \end{align*}
よって
\begin{align*} A = \begin{pmatrix} 2 & 3 \\ 1 & -5 \\ 7 & 6 \end{pmatrix} \end{align*}